Raízes e radicais matematicas

Já sabemos que 6² = 36. Aprenderemos agora a operação que nos permite determinar qual o número que elevado ao quadrado equivale a 36.

, pois 6 elevado ao quadrado é 36.

Essa operação é a inversa da potenciação e denomina-se radiciação.

Outros exemplos:

, pois 2³ = 8.
, pois .

Sendo assim:

Notação

Leitura

 (lê-se “raiz quadrada de 81”)
 (lê-se “raiz cúbica de 64”)

Observação:
Na indicação de raiz quadrada, podemos omitir o índice 2. Por exemplo, .

Raízes de índice par

Quando elevamos um número positivo ou um número negativo a um expoente par, o resultado sempre é um número positivo.

Exemplo:

(-4)² = (-4)(-4) = 16

e

(+4)² = (+4)(+4) = 16

Porém, como em matemática o resultado de uma operação deve ser único, fica definido que:

Genericamente:

Qualquer raiz de índice par de um número positivo é o número positivo que elevado ao expoente correspondente a esse indíce equivale ao número dado.

Observação:

Não existe raiz real de um número negativo se o índice for par.

Exemplo:

 não existe, pois não há nenhum número real que elevado ao quadrado dê - 4.

Raízes de índice ímpar

Quando o índice de uma raiz é ímpar e o radicando é positivo, a raiz é positiva.

Quando o índice de uma raíz é ímpar e o radicando é negativo, a raiz é negativa.

Exemplos:

Propriedades dos radicais

Propriedade	Justificativa	Exemplo
	Escrevendo em forma de potência com expoente fraccionário:

Propriedades operatórias dos radicais

Propriedade		Justificativa	Exemplo
Radical de um produto
Radical de um quociente
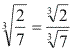Mudança de índice