1. Definição de 
| Definição Para um número real a e um inteiro positivo n (n ³ 2), definimos  =  . |
Exemplos
não representa um número pois 
não tem resultado de numero reais (!)
2. Definição de 
Nós podemos ampliar a definição de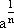 
para expoentes fraccionário com numeradores distintos de 1. Por exemplo, se escrevermos 
como 
, temos
para expoentes fraccionário com numeradores distintos de 1. Por exemplo, se escrevermos como , temos
Veja que simplificamos e levando ao cubo a raiz quadrada de 16. Essa simplificação também poderia ser feita extraindo a raiz quadrada do cubo de 16.
e levando ao cubo a raiz quadrada de 16. Essa simplificação também poderia ser feita extraindo a raiz quadrada do cubo de 16.| Definição Sejam m e n inteiros positivos, com n ³ 2. Se a é um número para o qual existe , então Também,  |
Exemplos
0 comentários:
Enviar um comentário