Conversão de múltiplos e submúltiplos

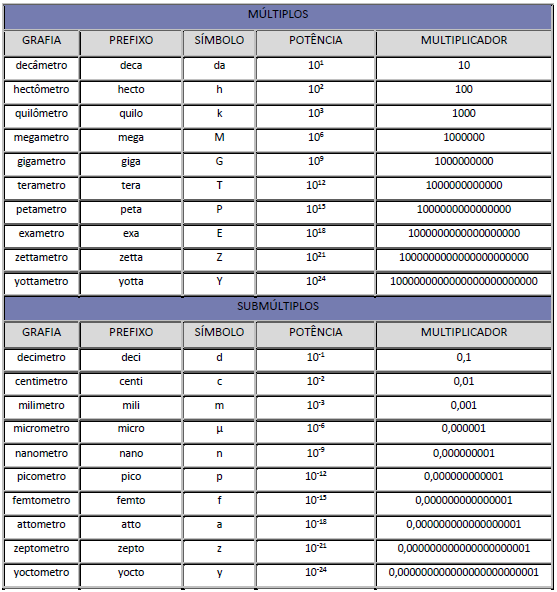
MÚLTIPLOS E SUBMÚLTIPLOS DO SISTEMA INTERNACIONAL

• Há que ter atenção às unidades que se escrevem em minúsculas e às unidades que se escrevem em maiúsculas.

Para convertermos uma unidade menor numa unidade maior, ou seja, um submúltiplo num múltiplo, há que dividi-la por 10, 100, 1000, etc. , enquanto para converte-la numa unidade menor, ou seja, converter um múltiplo num submúltiplo, multiplica-se por 10, 100, 1000, etc.

Para entender melhor como passar de uma unidade para outra unidade apresento um quadro mostrando cada posição de cada unidade:

Do lado esquerdo da unidade encontram-se os múltiplos e do lado direito os submúltiplos. 

• Para passar de uma unidade para outra maior, retire os zeros (ou no caso de número decimal passar a virgula x casas para esquerda)

Por exemplo:

Ex:  12000 = 12 k (converter unidade para kilo)  – dividiu-se por 1000, ou retirou-se três zeros

Ex:  123456,7 = 123,4567 k (converter unidades para kilo) – como é um número decimal deslocamos a vírgula três posições para esquerda.

• para passar de uma unidade para outra menor, acrescente os zeros (ou no caso de número decimal passar a vírgula x casas para direita).

Por exemplo:

Ex: 12 k = 12000   (converter kilo para unidade) – multiplicou-se por 1000, ou acrescentou-se três zeros
Ex: 123,4567 k = 123456,7 (converter kilo para unidades) – como é um número decimal deslocamos três casas decimais para direita

- Pode-se verificar na tabela que da unidade “k” (kilo) à "unidade" há três casas (ou três zeros)

Pegando no exemplo anterior e para compreendermos melhor isto das unidades:

12 k = 12000000 m (acrescentámos 6 zeros pois da unidade “k” (kilo) até à unidade “m” (mili) há 6 casas).

12 kV = 12000000 mV (12 kilovolts = 12000000 milivolts)

12 km = 12000000 mm (12 kilometros = 12000000 milimetros)

USO DOS MÚLTIPLOS E SUBMÚLTIPLOS EM ELECTRÓNICA

Em electricidade e electrónica o uso de todos os múltiplos e submúltiplos que vimos não se aplica. De uma forma geral, podemos dizer que os múltiplos e submúltiplos usados em electrónica são os seguintes:

Assim facilita-se um pouco mais as coisas. Por isso, para passar de um submúltiplo para um múltiplo exactamente a seguir basta multiplicar por 1000 e para passar de um múltiplo para um submúltiplo exactamente anterior basta dividir por 1000.

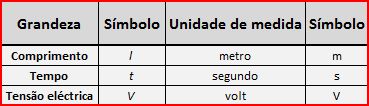
Resumindo o que disse atrás sobre grandezas e unidades apresento um quadro representando as grandezas, símbolos e unidades de medida que falei até aqui.

Como excepção à regra, os múltiplos da grandeza tempo não seguem o sistema decimal como nas outras grandezas, mas os submúltiplos sim. Assim os múltiplos do segundo serão:

• hora (h) = 60 minutos = 3600 segundos
• minuto (min) = 60 segundos

Os submúltiplos da grandeza tempo, tal como nas outras grandezas, são igualmente o décimo de segundo (ds), centésimo de segundo (cs), milisegundo (ms), microsegundo (µs), etc.

Read More

Força magnética sobre um fio conduto

Sempre que uma carga é posta sobre influência de um campo magnético, esta sofre uma interação que pode alterar seu movimento. Se o campo magnético em questão for uniforme, vimos que haverá uma força agindo sobre a carga com intensidade , onde  é o ângulo formado no plano entre os vetores velocidade e campo magnético. A direção e sentido do vetor  serão dadas pela regra da mão direita espalmada.

Se imaginarmos um fio condutor percorrido por corrente, haverá elétrons livres se movimentando por sua secção transversal com uma velocidade . No entanto, o sentido adotado para o vetor velocidade, neste caso, é o sentido real da corrente ( tem o mesmo sentido da corrente). Para facilitar a compreensão pode-se imaginar que os elétrons livres são cargas positivas.

Como todos os elétrons livres têm carga (que pela suposição adotada se comporta como se esta fosse positiva), quando o fio condutor é exposto a um campo magnético uniforme, cada elétron sofrerá ação de uma força magnética.

Mas se considerarmos um pequeno pedaço do fio ao invés de apenas um elétron, podemos dizer que a interação continuará sendo regida por , onde Q é a carga total no segmento do fio, mas como temos um comprimento percorrido por cada elétron em um determinado intervalo de tempo, então podemos escrever a velocidade como:

Ao substituirmos este valor em  teremos a força magnética no segmento, expressa pela notação :

Mas sabemos que  indica a intensidade de corrente no fio, então:

Sendo esta expressão chamada de Lei Elementar de Laplace.

A direção e o sentido do vetor  são perpendicular ao plano determinado pelos vetores  e , e pode ser determinada pela regra da mão direita espalmada, apontando-se o polegar no sentido da corrente e os demais dedos no sentido do vetor .

Saiba mais... Se quisermos determinar a força magnética que atua em fio extenso (com dimensões não desprezíveis) devemos fazer com que os comprimentos  sejam cada vez menores e somar os vetores em cada , de modo que toda o fio seja descrito, uma forma avançada para se realizar este cálculo é utilizando-se integral de linha. Para o caso particular onde o condutor é retilíneo, todos os vetores serão iguais, então podemos reescrever a Lei elementar de Laplace como .

Read More

Campo Magnético

Campo Magnético é a região próxima a um ímã que influencia outros ímãs ou materiais ferromagnéticos e paramagnéticos, como cobalto e ferro.

Compare campo magnético com campo gravitacional ou campo elétrico e verá que todos estes têm as características equivalentes.

Também é possível definir um vetor que descreva este campo, chamado vetor indução magnética e simbolizado por . Se pudermos colocar uma pequena bússola em um ponto sob ação do campo o vetor  terá direção da reta em que a agulha se alinha e sentido para onde aponta o polo norte magnético da agulha.

Se pudermos traçar todos os pontos onde há um vetor indução magnética associado veremos linhas que são chamadas linhas de indução do campo magnético. estas são orientados do polo norte em direção ao sul, e em cada ponto o vetor  tangencia estas linhas.

As linhas de indução existem também no interior do ímã, portanto são linhas fechadas e sua orientação interna é do polo sul ao polo norte. Assim como as linhas de força, as linhas de indução não podem se cruzar e são mais densas onde o campo é mais intenso.

Campo Magnético Uniforme

De maneira análoga ao campo elétrico uniforme, é definido como o campo ou parte dele onde o vetor indução magnética é igual em todos os pontos, ou seja, tem mesmo módulo, direção e sentido. Assim sua representação por meio de linha de indução é feita por linhas paralelas e igualmente espaçadas.

A unidade de campo magnético no S.I. é chamada de tesla (T):

Fontes de campo magnético

·        Campo magnético gerado por cargas puntiformes em movimento. 

Quando uma carga q se move com velocidade v, gera, no espaço, um campo magnético B dado por:

                                           

onde µ_o é a permeabilidade magnética do vácuo e µ_o = 4p.10^-7 T.m/A = 4p.10^-7 N/A²

·        Lei de Biot-Savart

                Campo magnético gerado por um elemento de corrente elétrica:

      O sentido do campo magnético é dado pela regra da mão direita, com o polegar no sentido da corrente elétrica e os dedos segurando o fio indicam o sentido do campo. 

Campo magnético gerado por uma corrente elétrica em um fio longo e retilíneo:

                                               

onde R é a distância perpendicular do fio ao ponto P.

Campo Magnético no centro de uma espira circular de raio R:

Campo magnético, no eixo de uma espira, a uma distância x do seu centro:

Bobina ou Solenóide: Ambos são agrupamentos de espiras, mas na prática, há algumas pequenas diferenças. Bobina tem um significado genérico. Qualquer enrolamento, não importa o formato, é uma bobina. Solenóide tem um significado mais restrito. Em geral, esta denominação é usada para conjuntos de espiras circulares enroladas uniformemente em espiral.

Campo Magnético no centro de uma bobina plana com N espiras:

Campo magnético no centro de um solenóide comprido:

Read More

Ímãs e magnetos

Um ímãn é definido com um objeto capaz de criar um campo magnético à sua volta e pode ser natural ou artificial. Um ímãn natural é feito de minerais com substâncias magnéticas, como por exemplo, a magnetita, e um ímã artificial é feito de um material sem propriedades magnéticas, mas que pode adquirir permanente ou instantaneamente características de um ímãn natural. Os ímãs artificiais também são subdivididos em: permanentes, temporais ou eletroímãs. Um ímã permanente é feito de material capaz de manter as propriedades magnéticas mesmo após cessar o processo de imantação, estes materiais são chamados ferromagnéticos. Um ímã temporal tem propriedades magnéticas apenas enquanto se encontra sob ação de outro campo magnético, os materiais que possibilitam este tipo de processo são chamados paramagnéticos. Um eletroímã é um dispositivo composto de um condutor por onde circula corrente elétrica e um núcleo, normalmente de ferro. Suas características dependem da passagem de corrente pelo condutor; ao cessar a passagem de corrente cessa também a existência do campo magnético. Propriedades dos ímãs Polos magnéticos São as regiões onde se intensificam as ações magnéticas. Um ímãn é composto por dois polos magnéticos, norte e sul, normalmente localizados em suas extremidades, exceto quando estas não existirem, como em um ímãn em forma de disco, por exemplo. Por esta razão são chamados dipolos magnéticos. Para que sejam determinados estes polos, se deve suspender o ímã pelo centro de massa e ele se alinhará aproximadamente ao polo norte e sul geográfico recebendo nomenclatura equivalente. Desta forma, o polo norte magnético deve apontar para o polo norte geográfico e o polo sul magnético para o polo sul geográfico. Atração e repulsão Ao manusear dois ímãs percebemos claramente que existem duas formas de colocá-los para que estes sejam repelidos e duas formas para que sejam atraídos. Isto se deve ao fato de que polos com mesmo nome se repelem, mas polos com nomes diferentes se atraem, ou seja: Esta propriedade nos leva a concluir que os polos norte e sul geográficos não coincidem com os polos norte e sul magnéticos. Na verdade eles se encontram em pontos praticamente opostos, como mostra a figura abaixo: A inclinação dos eixos magnéticos em relação aos eixos geográficos é de aproximadamente 191°,  fazendo com os seus polos sejam praticamente invertidos em relação aos polos geográficos. Interação entre polos Dois polos se atraem ou se repelem, dependendo de suas características, à razão inversa do quadrado da distância  entre eles. Ou seja, se uma força de interação F é estabelecida a uma distância d, ao dobrarmos esta distância a força observada será igual a uma quarta parte da anterior F/4. E assim sucessivamente. Inseparabilidade dos polos de um ímã Esta propriedade diz que é impossível separar os polos magnéticos de um ímã, já que toda vez que este for dividido serão obtidos novos polos, então se diz que qualquer novo pedaço continuará sendo um dipolo magnético.

Read More

Consumo de energia elétrica

A energia elétrica pode ser definida como a capacidade de trabalho de uma corrente elétrica.

Cada aparelho que utiliza a eletricidade para funcionar, como por exemplo, o computador de onde você lê esse texto, consome uma quantidade de energia elétrica.

Para calcular este consumo basta sabermos a potência do aparelho e o tempo de utilização dele, por exemplo, se quisermos saber quanta energia gasta um chuveiro de 5500W ligado durante 15 minutos, seu consumo de energia será:

Mas este cálculo nos mostra que o joule (J) não é uma unidade eficiente neste caso, já que o cálculo acima se refere a apenas um banho de 15 minutos, imagine o consumo deste chuveiro em uma casa com 4 moradores que tomam banho de 15 minutos todos os dias no mês.

Para que a energia gasta seja compreendida de uma forma mais prática podemos definir outra unidade de medida, que embora não seja adotada no SI, é mais conveniente.

Essa unidade é o quilowatt-hora (kWh).

Para calcularmos o consumo do chuveiro do exemplo anterior nesta unidade consideremos sua potência em kW e o tempo de uso em horas, então teremos:

O mais interessante em adotar esta unidade é que, se soubermos o preço cobrado por kWh, podemos calcular quanto será gasta em dinheiro por este consumo.

Read More

Efeito Joule e potência elétrica

Efeito Joule

A corrente elétrica é resultado de movimentação de aniões, catiões ou eletrões livres, como já vimos. Ao existir corrente elétrica as partículas que estão em movimento acabam colidindo com as outras partes do condutor que se encontra em repouso, causando uma excitação que por sua vez irá gerar um efeito de aquecimento. A este efeito dá-se o nome efeito Joule.

O aquecimento no fio pode ser medido pela lei de joule, que é matematicamente expressa por:

Esta relação é valida desde que a intensidade da corrente seja constante durante o intervalo de tempo de ocorrência.

Potência elétrica

 A potência elétrica dissipada por um condutor é definida como a quantidade de energia térmica que passa por ele durante uma quantidade de tempo.

A unidade utilizada para energia é o watt (W), que designa joule por segundo (J/s)

Ao considerar que toda a energia perdida em um circuito é resultado do efeito Joule, admitimos que a energia transformada em calor é igual a energia perdida por uma carga q que passa pelo condutor. Ou seja:

Mas sabemos que:

Então:

Logotipo:

Mas sabemos que , então podemos escrever que:

Por exemplo:

Qual a corrente que passa em uma lâmpada de 60W em uma cidade onde a tensão na rede elétrica é de 220V?

Pela 1ª Lei de Ohm temos que , então podemos definir duas formas que relacionem a potência elétrica com a resistência.

Então se utilizando do exemplo anterior, qual a resistência do filamento interno da lâmpada?

Read More