Também conhecido como movimento acelerado, consiste em um movimento onde há variação de velocidade, ou seja, o móvel sofre aceleração à medida que o tempo passa.
Mas se essa variação de velocidade for sempre igual em intervalos de tempo iguais, então dizemos que este é um Movimento Uniformemente Variado (também chamado de Movimento Uniformemente Acelerado), ou seja, que tem aceleração constante e diferente de zero.
O conceito físico de aceleração, difere um pouco do conceito que se tem no cotidiano. Na física, acelerar significa basicamente mudar de velocidade, tanto tornando-a maior, como também menor. Já no cotidiano, quando pensamos em acelerar algo, estamos nos referindo a um aumento na velocidade.
O conceito formal de aceleração é: a taxa de variação de velocidade numa unidade de tempo, então como unidade teremos:
Aceleração
Assim como para a velocidade, podemos definir uma aceleração média se considerarmos a variação de velocidade ᐃv em um intervalo de tempo ᐃt, e esta média será dada pela razão:
Velocidade em função do tempo
No entanto, quando este intervalo de tempo for infinitamente pequeno, ou seja, ᐃt→0, tem-se a aceleração instantânea do móvel.
Isolando-se o ᐃv:
Mas sabemos que:
Então:
Entretanto, se considerarmos t0=0, teremos a função horária da velocidade do Movimento Uniformemente Variado, que descreve a velocidade em função do tempo [v=f(t)]:
Posição em função do tempo
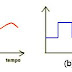
A melhor forma de demonstrar esta função é através do diagrama velocidade versus tempo (v x t) no movimento uniformemente variado.
O deslocamento será dado pela área sob a reta da velocidade, ou seja, a área do trapézio.
Onde sabemos que:
logo:
ou
Interpretando esta função, podemos dizer que seu gráfico será uma parábola, pois é resultado de uma função do segundo grau.
Equação de Torricelli
Até agora, conhecemos duas equações do movimento uniformemente variado, que nos permitem associar velocidade ou deslocamento com o tempo gasto. Torna-se prático encontrar uma função na qual seja possível conhecer a velocidade de um móvel sem que o tempo seja conhecido.
Para isso, usaremos as duas funções horárias que já conhecemos:
Isolando-se t em (1):
Substituindo t em (2) teremos:
Reduzindo-se a um denominador comum:
Exemplo:
(UFPE) Uma bala que se move a uma velocidade escalar de 200m/s, ao penetrar em um bloco de madeira fixo sobre um muro, é desacelerada até parar. Qual o tempo que a bala levou em movimento dentro do bloco, se a distância total percorrida em seu interior foi igual a 10cm?
Apesar de o problema pedir o tempo que a bala levou, para qualquer uma das funções horárias, precisamos ter a aceleração, para calculá-la usa-se a Equação de Torricelli.
Observe que as unidades foram passadas para o SI (10cm=0,1m)
A partir daí, é possível calcular o tempo gasto:




































Enviar um comentário