Estática de um corpo rígido

Chamamos de corpo rígido ou corpo extenso, todo o objeto que não pode ser descrito por um ponto.

Para conhecermos o equilíbrio nestes casos é necessário estabelecer dois conceitos:

Centro de massa

Um corpo extenso pode ser considerado um sistema de partículas, cada uma com sua massa.

A resultante total das massas das partículas é a massa total do corpo. Seja CM o ponto em que podemos considerar concentrada toda a massa do corpo, este ponto será chamado Centro de Massa do corpo.

Para corpos simétricos, que apresentam distribuição uniforme de massa, o centro de massa é o próprio centro geométrico do sistema. Como no caso de uma esfera homogênea, ou de um cubo perfeito.

Para os demais casos, o cálculo do centro de massa é feito através da média aritmética ponderada das distâncias de cada ponto do sistema.

Para calcularmos o centro de massa precisamos saber suas coordenadas em cada eixo do plano cartesiano acima, levando em consideração a massa de cada partícula:

Então o Centro de Massa do sistema de partículas acima está localizado no ponto (1,09 , 0,875), ou seja:

Como forma genérica da fórmula do centro de massa temos:

Momento de uma força

Imagine uma pessoa tentando abrir uma porta, ela precisará fazer mais força se for empurrada na extremidade contrária à dobradiça, onde a maçaneta se encontra, ou no meio da porta?

Claramente percebemos que é mais fácil abrir ou fechar a porta se aplicarmos força em sua extremidade, onde está a maçaneta. Isso acontece, pois existe uma grandeza chamada Momento de Força 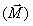, que também pode ser chamado Torque.

Esta grandeza é proporcional a Força e a distância da aplicação em relação ao ponto de giro, ou seja:

A unidade do Momento da Força no sistema internacional é o Newton-metro (N.m)

Como este é um produto vetorial, podemos dizer que o módulo do Momento da Força é:

Sendo:

M= Módulo do Momento da Força.

F= Módulo da Força.

d=distância entre a aplicação da força ao ponto de giro; braço de alavanca.

sen θ=menor ângulo formado entre os dois vetores.

Como , se a aplicação da força for perpendicular à d o momento será máximo;

Como , quando a aplicação da força é paralela à d, o momento é nulo.

E a direção e o sentido deste vetor são dados pela Regra da Mão Direita.

O Momento da Força de um corpo é:

• Positivo quando girar no sentido anti-horário;
• Negativo quando girar no sentido horário;

Exemplo:

Qual o momento de força para uma força de 10N aplicada perpendicularmente a uma porta 1,2m das dobradiças?

Condições de equilíbrio de um corpo rígido

Para que um corpo rígido esteja em equilíbrio, além de não se mover, este corpo não pode girar. Por isso precisa satisfazer duas condições:

1. O resultante das forças aplicadas sobre seu centro de massa deve ser nulo (não se move ou se move com velocidade constante).
2. O resultante dos Momentos da Força aplicadas ao corpo deve ser nulo (não gira ou gira com velocidade angular constante).

Tendo as duas condições satisfeitas qualquer corpo pode ficar em equilíbrio, como esta caneta:

Exemplo:

(1) Em um circo, um acrobata de 65kg se encontra em um trampolim uniforme de 1,2m, a massa do trampolim é 10kg. A distância entre a base e o acrobata é 1m. Um outro integrante do circo puxa uma corda presa à outra extremidade do trampolim, que está a 10cm da base. Qual a força que ele tem de fazer para que o sistema esteja em equilíbrio.

Como o trampolim é uniforme, seu centro de massa é exatamente no seu meio, ou seja, a 0,6m. Então, considerando cada força:

Pela segunda condição de equilíbrio: