Esta forma de dilatação consiste em um caso onde há dilatação linear em duas dimensões.
Considere, por exemplo, uma peça quadrada de lados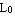 
que é aquecida uma temperatura 
, de forma que esta sofra um aumento em suas dimensões, mas como há dilatação igual para os dois sentidos da peça, esta continua quadrada, mas passa a ter lados L.
que é aquecida uma temperatura , de forma que esta sofra um aumento em suas dimensões, mas como há dilatação igual para os dois sentidos da peça, esta continua quadrada, mas passa a ter lados L.
Podemos estabelecer que:
assim como:
E relacionando com cada lado podemos utilizar:
Para que possamos analisar as superfícies, podemos elevar toda a expressão ao quadrado, obtendo uma relação com suas áreas:
Mas a ordem de grandeza do coeficiente de dilatação linear (α) é 
, o que ao ser elevado ao quadrado passa a ter grandeza 
, sendo imensamente menor que α. Como a variação da temperatura (Δθ) dificilmente ultrapassa um valor de 10³ºC para corpos no estado sólido, podemos considerar o termo α²Δθ² desprezível em comparação com 2αΔθ, o que nos permite ignorá-lo durante o cálculo, assim:
, o que ao ser elevado ao quadrado passa a ter grandeza , sendo imensamente menor que α. Como a variação da temperatura (Δθ) dificilmente ultrapassa um valor de 10³ºC para corpos no estado sólido, podemos considerar o termo α²Δθ² desprezível em comparação com 2αΔθ, o que nos permite ignorá-lo durante o cálculo, assim:
Mas, considerando-se:
Onde, β é o coeficiente de dilatação superficial de cada material, têm-se que:
Observe que esta equação é aplicável para qualquer superfície geométrica, desde que as áreas sejam obtidas através das relações geométricas para cada uma, em particular (circular, retangular, trapezoidal, etc.).
Exemplo:
(1) Uma lâmina de ferro tem dimensões 10m x 15m em temperatura normal. Ao ser aquecida 500ºC, qual será a área desta superfície? Dado: 
Enviar um comentário